Non-ideal MHD and the Formation & Fragmentation of Protostellar Disks

Using numerical simulations, our group explores the effect of magnetic fields on disk formation, evolution, substructure, and grain growth within the disks. The relative strengths of non-ideal MHD effects determine whether a disk can form at all, as well as the orientation of the disk. Ambipolar diffusion, one important non-ideal MHD effect, removes small grains from the disk, which in turn changes the ambipolar diffusivity and promotes disk formation. The growth of larger grains also depends on the magnetic field: the magneto-rotational instability generates turbulence in the disk, which can result in much faster grain growth compared to the hydrodynamic Kolmogorov turbulence. Finally, the interplay between the magnetic field and the grain growth creates a wealth of substructures in the disks, carving out gaps and rings, where planet formation may occur.

The interplay between non-ideal MHD effects in protoplanetary disk formation

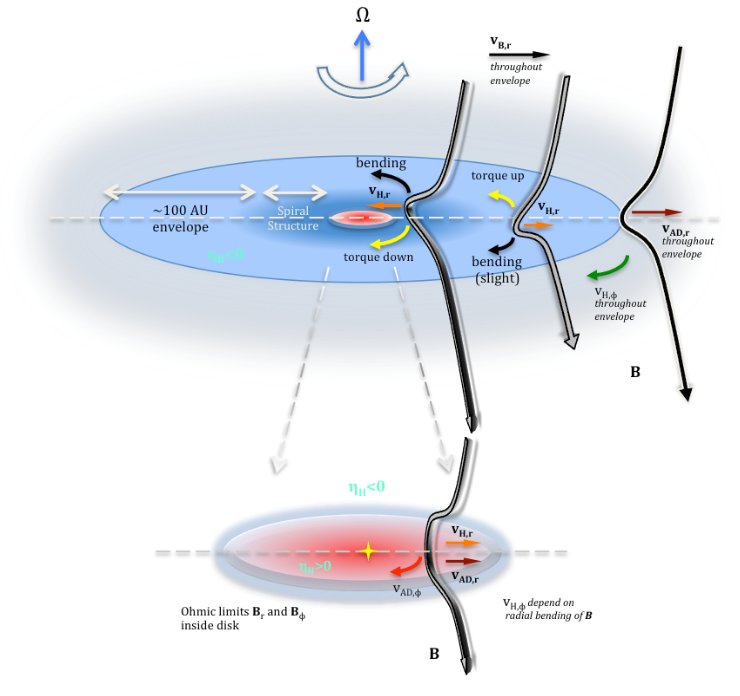
The formation of rotationally supported disks (RSDs) was previously shown to be difficult due to the so-called magnetic braking “catastrophe". By carefully investigating the ionization chemical network, we uncovered a unified picture of protostellar collapse in which non-ideal MHD effects work together in the diffusion of the magnetic field, allowing the formation of RSDs for typical prestellar core conditions. Based on our previous results of the depletion of very small grains (VSGs≤100 Å; Zhao et al. 2016, Silsbee et al. 2020) in protostellar envelope, we further investigated the intricate interplay between the non-ideal MHD effects, especially for ambipolar diffusion (AD) and Hall effect (Zhao et al. 2020, 2021), in the protostellar envelopes and disks. We discovered that despite the dispersive nature of the Hall effect which may counteract the diffusion of magnetic fields by AD and Ohmic dissipation, the net effect of non-ideal MHD in the protostellar envelope is to move the magnetic field radially outward against collapse (see Figure 1). As a result, disk formation should be relatively common for typical prestellar core conditions, with the observed range of cosmic-ray ionization rate (few 10-18 /s to few 10-16 /s; Caselli et al. 1998; Padovani et al. 2009). We also find that the magnetic field polarity does not affect disk formation, but can cause the disk to rotate in either retrograde or prograde fashion with respect to its surrounding envelope, if microphysics favors a strong Hall effect.

Figure 1. Sketch of magnetic field morphologies and non-ideal MHD drift velocities in the inner envelope (top) and in the disk (bootom) for the ant-aligned case, in the Hall-dominated collapse. Note that Hall diffusivity changes sign across the disc boundary. Adapted from Zhao et al. (2020). — **Figure 1.** Sketch of magnetic field morphologies and non-ideal MHD drift velocities in the inner envelope (top) and in the disk (bootom) for the ant-aligned case, in the Hall-dominated collapse. Note that Hall diffusivity changes sign across the disc boundary. Adapted from Zhao et al. (2020).

**Figure 1.** Sketch of magnetic field morphologies and non-ideal MHD drift velocities in the inner envelope (top) and in the disk (bootom) for the ant-aligned case, in the Hall-dominated collapse. Note that Hall diffusivity changes sign across the disc boundary. Adapted from Zhao et al. (2020).

Depletion of small dust grains by ambipolar diffusion

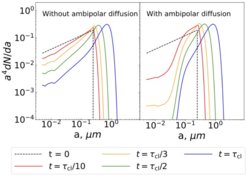
We explored a novel mechanism for the removal of small dust grains in molecular clouds and prestellar cores. In poorly ionized regions of the interstellar medium, there is typically motion between ionized and neutral species, termed ambipolar diffusion. In prestellar cores, grains smaller than a few tens of nanometers across are typically tied to the magnetic field lines, while larger grains are dragged inwards across the field lines by the neutral gas. This results in a relative velocity, typically several tens of meters per second, between large and small grains, causing the small grains to paste themselves onto the larger ones. We showed in Silsbee et al. (2020) that in the absence of any grain fragmentation, proper accounting for ambipolar diffusion in calculating grain motions results in the near-complete removal of grains smaller than ~20 nm in a prestellar core (see Figure 2). This work justifies the consideration of models such as in Zhao et al. (2020, 2021), in which the smallest grains are assumed to be entirely absent from the size distribution.

Figure 2. Evolution of the dust size distribution with and without ambipolar diffusion. In both cases, grain velocities arising from gas turbulence and Brownian motion were considered. Different color curves correspond to different amounts of time over which the size distribution has evolved, in units of the estimated cloud lifetime τcl. It is apparent that with ambipolar diffusion, the smallest grains are nearly completely removed in a small fraction of the cloud lifetime. Adapted from Silsbee et al. (2020). — ***Figure 2.*** Evolution of the dust size distribution with and without ambipolar diffusion. In both cases, grain velocities arising from gas turbulence and Brownian motion were considered. Different color curves correspond to different amounts of time over which the size distribution has evolved, in units of the estimated cloud lifetime τcl. It is apparent that with ambipolar diffusion, the smallest grains are nearly completely removed in a small fraction of the cloud lifetime. Adapted from Silsbee et al. (2020).

***Figure 2.*** Evolution of the dust size distribution with and without ambipolar diffusion. In both cases, grain velocities arising from gas turbulence and Brownian motion were considered. Different color curves correspond to different amounts of time over which the size distribution has evolved, in units of the estimated cloud lifetime τcl. It is apparent that with ambipolar diffusion, the smallest grains are nearly completely removed in a small fraction of the cloud lifetime. Adapted from Silsbee et al. (2020).

Magneto-rotational instability and grain growth

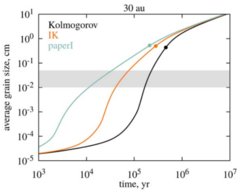
Grain growth in protoplanetary disks is the first step towards planet formation. One of the most important pieces in the grain growth model is calculating the collisional velocity between two grains in turbulent gas. The collisional velocities in previous works are obtained based on the assumption that the turbulence is hydrodynamic with the Kolmogorov power spectrum. However, realistic protoplanetary disks are magnetized, and turbulent motions can be induced by the magneto-rotational instabilities (MRI). In Gong et al. (2020), we use magneto-hydrodynamic (MHD) simulations of MRI to investigate turbulence properties in protoplanetary disks. We observe a persistent kinetic energy spectrum of 4/3, shallower than the Kolmogorov spectrum of 5/3. In our subsequent work of Gong et al. (2021), we study the impact of turbulence properties on grain collisional velocities, and find that for the modeled cases of the Iroshnikov-Kraichnan turbulence and the turbulence induced by the magneto-rotational instabilities, collisional velocities of small grains are much larger than those for the standard Kolmogorov turbulence. This leads to faster grain coagulation in the outer regions of protoplanetary disks, resulting in rapid increase of dust opacity in mm-wavelength and possibly promoting planet formation in very young disks (Figure 3).

Figure 3. Evolution of the average grain size in the disk midplane at 30 AU, for Kolmogorov (black), Iroshnikov-Kraichnan (orange) and MRI (green) turbulence. The gray shaded region marks the size range that contributes the most to the dust emission at millimeter wavelengths. The filled circles indicate radial drift barriers for each turbulence model. Compared to the standard Kolmogorov turbulence assumption, MRI turbulence results in faster coagulation of small grains, possibly promoting planet formation. Adapted from Gong et al. (2021). — ***Figure 3.*** Evolution of the average grain size in the disk midplane at 30 AU, for Kolmogorov (black), Iroshnikov-Kraichnan (orange) and MRI (green) turbulence. The gray shaded region marks the size range that contributes the most to the dust emission at millimeter wavelengths. The filled circles indicate radial drift barriers for each turbulence model. Compared to the standard Kolmogorov turbulence assumption, MRI turbulence results in faster coagulation of small grains, possibly promoting planet formation. Adapted from Gong et al. (2021).

***Figure 3.*** Evolution of the average grain size in the disk midplane at 30 AU, for Kolmogorov (black), Iroshnikov-Kraichnan (orange) and MRI (green) turbulence. The gray shaded region marks the size range that contributes the most to the dust emission at millimeter wavelengths. The filled circles indicate radial drift barriers for each turbulence model. Compared to the standard Kolmogorov turbulence assumption, MRI turbulence results in faster coagulation of small grains, possibly promoting planet formation. Adapted from Gong et al. (2021).

Effects of non-ideal MHD on ring formation

Radial substructures have now been observed in a wide range of proto-planetary disks (PPDs), from young to old systems, however, the mechanism of formation of these structures is still an area of vigorous debate. Recent magnetohydrodynamic (MHD) simulations have shown that rings and gaps can form naturally in PPDs when parameterized non-ideal MHD effects are included (e.g. Suriano et al 2018, Riols & Lesur 2019). In Nolan et al 2022 we remove the parameterization of these terms by including simple chemistry and grain modeling to calculate the non-ideal effects in a more self-consistent way. Including ambipolar diffusion, we find that large grain populations (> 1 μm), and those including a population of very small polyaromatic hydrocarbons (PAHs) facilitate the growth of periodic, stable rings, while intermediate-sized grains suppress ring formation. Including Ohmic diffusion removes the positive influence of PAHs, with only large grain populations still producing periodic ring and gap structures. We aim next to include Hall diffusion and more accurate chemistry modeling, to determine whether non-ideal effects can reproduce the ring structures seen in PPDs.

Figure 4. Face-on surface density profiles normalized to their initial radial distribution (out to a radius of 35 au) at t/t0=2500, for grain distributions of increasing size, from 0.005-1 um (MRN) to 1-100um (eMRN). Adapted from Nolan et al. (2022). — ***Figure 4***. Face-on surface density profiles normalized to their initial radial distribution (out to a radius of 35 au) at t/t0=2500, for grain distributions of increasing size, from 0.005-1 um (MRN) to 1-100um (eMRN). Adapted from Nolan et al. (2022).

***Figure 4***. Face-on surface density profiles normalized to their initial radial distribution (out to a radius of 35 au) at t/t0=2500, for grain distributions of increasing size, from 0.005-1 um (MRN) to 1-100um (eMRN). Adapted from Nolan et al. (2022).

Selected References

Gong, M., Ivlev, A. V., Akimkin, V., Caselli, P., 2021, ApJ, 917, 82
Gong, M., Ivlev, A. V., Zhao, B., Caselli, P. 2020, ApJ, 891, 172
Nolan, C. A., Zhao, B., Caselli, P. 2022, in preparation
Silsbee, K., Ivlev A. V., Sipilä, O,. Caselli, P., & Zhao, B. 2020 A&A, 641, 39
Zhao, B. et al., 2020, MNRAS, 492, 3375
Zhao, B. et al., 2021, MNRAS, 505, 5142