Dark Matter

Credit: NASA, ESA, Richard Ellis (Caltech) and Jean-Paul Kneib (Observatoire Midi-Pyrenees, France) Acknowledgment: NASA, A. Fruchter and the ERO Team (STScI and ST-ECF)
Dynamics:
We probe the dark matter halos of early-type galaxies by stellar dynamics, by measuring the mean motions of their stars and reconstructing the gravitational potentials that generate them. Recently we have measured the densities of dark matter halos in elliptical galaxies of different luminosity and studied their scaling relations, to constrain when they assembled. We also study the masses, ages and formation histories of different bulge types in spiral galaxies. For example, the bulge of M31 is old and more massive than one had estimated, and the kinematics of bulges allows one to distinguish between a classical and a pseudo-bulge.
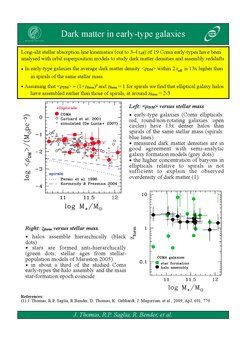
SM Scaling Relations of Early-Type Galaxies
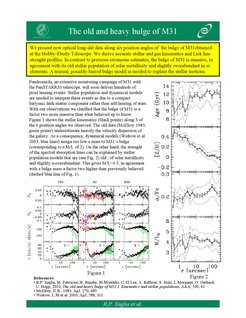
The old and massive bulge of M31
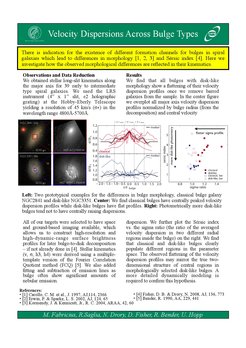
Kinematics of bulges
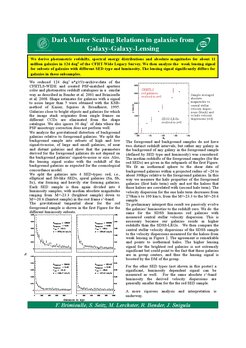
DM Scaling Relations in Galaxies from Galaxy-Galaxy Lensing
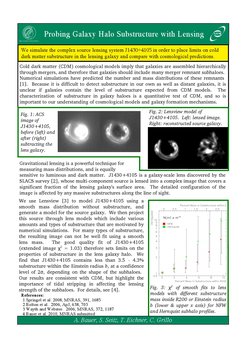
Halo Substructure in Ellipticals from Gravitational Lensing
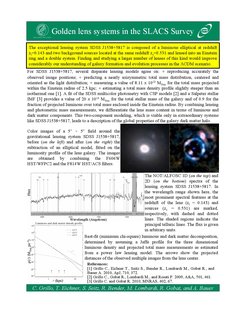
Golden Lens Systems
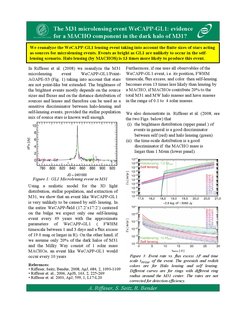
Pixellensing Towards M31: WECAPP GL1

Constraints on MACHOS in M31 from 12 Pixellensing Events

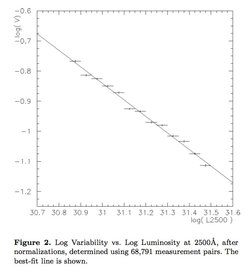
CARS: the CFHTLS-Archive-Research Survey. I. Five-band multi-colour data from 37 sq. deg. CFHTLS-wide observations
Astronomy and Astrophysics 493, 1197
Photometric mass and mass decomposition in early-type lens galaxies
Astronomy and Astrophysics 501, 461
Golden Gravitational Lensing Systems from the Sloan Lens ACS Survey. I. SDSS J1538+5817: One Lens for Two Sources
Astrophysical Journal 710, 372
Finite-Source Effects in Microlensing: A Precise, Easy to Implement, Fast, and Numerically Stable Formalism
http://adsabs.harvard.edu/abs/2009ApJ...695..200L
Properties of M31. I. Dust: Basic properties and a discussion about age-dependent dust heating
Astronomy and Astrophysics 507, 283
The HST/ACS Coma Cluster Survey - V. Compact stellar systems in the Coma Cluster
Monthly Notices of the Royal Astronomical Society 397, 1816
The old and heavy bulge of M 31 . I. Kinematics and stellar populations
Astronomy and Astrophysics 509, 61
The flattening and the orbital structure of early-type galaxies and collisionless N-body binary disc mergers
Monthly Notices of the Royal Astronomical Society 393, 641
Dark Matter Scaling Relations and the Assembly Epoch of Coma Early-Type Galaxies
Astrophysical Journal 691, 770











