General Relativity
The Galactic Center with its supermassive black hole Sagittarius A* (Sgr A*) and its extreme gravitational potential offers a unique possibility to study effects of general relativity. We use the stars in close orbits around the black hole, especially S2, to find deviations from Newtonian gravity and test general relativity in different ways.
Measurement of Gravitational Redshift in the Galactic Center
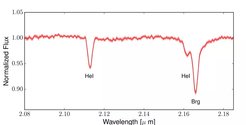
With a distance of 27,000 light-years from earth and an apparent Schwarzschild radius of 53 µm, Sgr A* is the closest of its kind and the largest in the sky. It is surrounded by a cluster of high-velocity stars, called the S-stars, whose trajectories are governed by the gravitational field of the black hole. We used the Very Large Telescope (VLT) instruments GRAVITY and SINFONI to follow the short (16-year) orbit star S2 during its recent pericenter passage in May 2018, and collected astrometric and spectroscopic data, respectively. For the first time, these joint data allowed for a robust detection of the combined gravitational redshift and transverse Doppler effect on S2.
Gravitational redshift is one of the three classic tests of general relativity. Einstein's theory foresees that due to the gravitational time dilation, a light beam is stretched to longer wavelengths by a gravitational field. The observed change in the wavelength of light from S2 is inconsistent with Newtonian predictions and in excellent agreement with Einstein's general theory of relativity. On a technological level, the signature of general relativity here is purely spectroscopic. However, the excellent astrometry from GRAVITY is crucial, as it helps determine the orbital motion to a degree of precision that breaks the degenarcy between the gravitational redshift, and find a different Kepler orbit, mimicking the redshift signal.

Source: GRAVITY Collaboration, 2018A&A...615L..15G and newer data
Einstein Equivalence Principle
One of the cornerstones of general relativity is the Einstein Equivalence Principle. It consists of three parts: the weak equivalence principle, the local Lorentz invariance, and the local position invariance. In Amorim et al. 2019, we use the orbit of S2 to test the local position invariance (LPI), which states that the results of a nongravitational experiment are independent of the position in space-time.
The star S2 experiences very strong changes in gravitational potential on its eccentric orbit around the supermassive black hole Sgr A*. In the three years leading up to the pericenter passage of S2, the gravitational potential experienced by the star changes by four orders of magnitude, which makes it a unique probe and allows us to test the LPI. This is possible by observing the redshift from two different atomic lines, hydrogen and helium. During the pericenter passage, we did not detect a different behavior of the two absorption lines, which allows us to put a limit on violations of the LPI to below 5%. While current tests on Earth are much more restrictive on that limit, our test in the Galactic Center laboratory, using stellar spectra and a supermassive black hole, charts a completely untested potential regime.
In an outlook, we also show that with the next-generation class of telescopes, such as the ELT, much more restrictive tests of the LPI and also the weak equivalence principle will be possible.
More information: Amorim et al. 2019, PhysRevLett.122.101102

Prograde Relativistic Precession of the S2 Orbit
While the gravitational redshift only affects the photons emitted by the star, other effects in general relativity also alter the motions of the star itself. Just as the Mercury orbit shows a measurable deviation from a Keplerian ellipse due to the Schwarzschild metric replacing the Newtonian gravitational field, the star S2 in orbit around Sgr A* displays a prograde precession. General relativity makes the orbital ellipse rotate in its plane by 12 arcminutes per revolution of 16 years. The effect manifests itself both in the astrometry and the spectroscopy, but due to the ultra-precise measurements with GRAVITY, the astrometric effect is easier to detect. In 2020, our team reported that the precession was observed in the 2019 S2 data exactly as predicted by general relativity with a significance of 5 sigma. Adding the 2020 and 2021 data confirms this result and enhances the significance to 7 sigma.
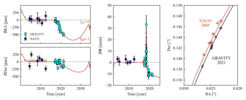
If some of the mass around Sgr A* were in the form of an unseen, extended component, one would observe a retrograde precession, opposite to what S2 shows. The fact that the orbital trace of S2 is well-described by general relativity allows us to place stringent limits on how much mass can be present inside the S2 orbit in an extended configuration: the maximum is a mere 4,000 solar masses or 0.1% of the mass of the black hole.
What Stellar Orbit is Needed to Measure the Spin of Sgr A* from Astrometric Data?
The spin of a black hole causes the entire space-time in its vicinity to be dragged along with the black hole rotation. This frame-dragging or Lens-Thirring effect is, however, a subtle quantity that affects the space-time only in the immediate vicinity of the source of gravity. Therefore, in order to measure the spin of a black hole with stellar orbits, a star must have a trajectory that passes closely enough to the black hole. In the case of the Galactic Center massive black hole, Sgr A*, observed with GRAVITY/VLT, a star requires a certain combination of semimajor axis, aorb, and eccentricity, e, to enable a spin measurement based on a number of N observations within T years. S2 turns out to be too far away from the black hole.
Stars that enable spin measurement are then expected on orbits with semimajor axes of a several hundred Schwarzschild radii. Using the current distributions of eccentricities and semimajor axes in the inner region of the Galactic Center, the estimated number of stars satisfying these conditions and bright enough to be seen is only about 0.12 for a 10-year observing campaign. Including radial velocity measurements with a precision of 50 km/s helps as this provides stronger constraints on the parameters and increases the number of expected stars by a factor of two (Waisberg et al. 2018, 2018MNRAS.476.3600W)
Hence, we aim at improving GRAVITY’s capabilities in the GRAVITY+ project, which will allow us to reach fainter magnitudes, increasing the chances of tracking a suitable star. Explicit simulations show that the most reliable way to measure the spin would be to complement GRAVITY+ astrometry with radial velocity data from spectroscopy, obtained with the future MICADO, a first-light instrument for the ELT.
The No-Hair Theorem
General relativity predicts that black holes can be fully described by three numbers only, they are said to have no hair: they can have mass, spin, and electric charge. The latter will always be close to zero in the plasma-rich astrophysical environment where Sgr A* resides. Hence, only mass and spin remain. The spin manifests itself primarily via the Lense-Thirring precession. However, it also deforms the symmetry of the gravitational field, leading in first order to a quadrupole moment. In general relativity, the quadrupole moment is fully given by the spin, as demanded by the no-hair theorem. Observationally, the quadrupole moment can be determined independently from the Lense-Thirring precession, and hence one can hope to compare the expected and measured quadrupole moment, constituting a first test ever of the no-hair theorem.
The key for that is again to be able to track stars on suitably short-period, highly elliptic orbits. GRAVITY+ and MICADO will be the instruments to look out for them.



