Kosmischer Mikrowellenhintergrund kein Gauss'sches Zufallsfeld?
Seit der eher zufälligen Entdeckung der Kosmischen Mikrowellenhintergrundstrahlung (oder kurz CMB) vor fast 50 Jahren, wird dieses gleichförmige Nachleuchten des Urknalls immer genauer untersucht. In den letzten 10 Jahren hat das WMAP-Weltraumobservatorium (Wilkinson-Microwave Anisotropy Probe) den CMB mit genügender Genauigkeit vermessen, so dass Wissenschaftler am Max-Planck-Institut für extraterrestrische Physik sowie anderen Instituten nach nicht-Gauss'schen Eigenschaften in der Strahlung suchen konnten. Neueste Ergebnisse deuten nun darauf hin, dass die Temperaturschwankungen, die man im CMB sehen kann, kein reines Gauss'sches Zufallsfeld sind, sondern dass es auf großen Skalen Korrelationen gibt. Dies könnte interessante Auswirkungen auf Inflationstheorien des sehr frühen Universums haben.
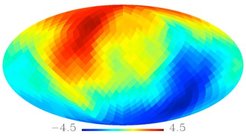
Copyright: C. Räth/MPE
Karte einer der Statistiken, die eingesetzt wird um nach nicht-Gaussianitäten in den WMAP-Daten zu suchen. Die Farbcodierung in dieser Karte für die größten Skalen zeigt an, dass es sehr signifikante Signaturen für nicht-Gaussianitäten und Asymmetrien gibt. Weitere unabhängige Untersuchungen werden zeigen, ob der kosmologische Ursprung des Signals bestätigt wird.
Copyright: C. Räth/MPE
Die kosmische Mikrowellenhintergrundstrahlung (CMB) ist die älteste beobachtbare Strahlung im Universum; sie wurde nur 380 000 Jahre nach dem Urknall ausgesandt, als der Kosmos durchsichtig wurde. Sie enthält daher wichtige Informationen über das sehr frühe Universum und hat schon sehr genaue Messungen des Alters, der Geometrie und des Materie- und Energiegehalts des Universums geliefert. Bei der Analyse des CMB wird meistens angenommen, dass die kleinen Temperaturfluktuationen wie ein Gauss'sches Zufallsfeld verteilt sind. Wenn das der Fall ist, so kann die Analyse auf das sogenannte "Leistungsspektrum" der Verteilung zurückgreifen, das die Menge der linearen Fluktuationen auf verschiedenen Skalen beschreibt - jegliche Information über Korrelationen höherer Ordnung wird hierbei nicht berücksichtigt.
Diese nicht-Gauss'schen Anteile könnten aber wichtige Informationen über die Phase der "Inflation" enthalten, einen Prozess im sehr frühen Universum, als das Universum sich nur winzige Bruchteile einer Sekunde nach dem Urknall extrem schnell ausdehnte. Während das Standardmodell für Inflation vorhersagt, dass die Fluktuationen nahezu perfekt Gauss-verteilt sind, so sagen komplexere Modelle signifikante Abweichungen von einem Gauss'schen Feld voraus.
Deshalb benutzten Christoph Räth und sein Team am Max-Planck-Institut für extraterrestrische Physik eine neue Methode um nach diesen nicht-Gaussianitäten zu suchen und sie zu quantifizieren, die für die Analyse des CMB angepasst wurde. "Wir benutzen eine statistische Analyse, die auf den sogenannten ‚Ersatz-' oder ‚Surrogat-Karten' basiert. Diese Methode ist in anderen Gebieten der Physik, die sich mit hoch komplexen, nicht-linearen Prozessen wie dem Klima oder dem Aktienmarkt beschäftigen, bereits wohlbekannt.", erklärt Räth. Wie in der herkömmlichen CMB-Analyse wird ein Leistungsspektrum aus den echten Daten erzeugt, das dann als Ausgangspunkt für die "Surrogat-Karten" dient, indem man zufällige, Gauss'sche Phasenkorrelationen annimmt. Mit geeigneten Statistiken kann man dann die Originaldaten mit den Surrogat-Karten vergleichen und Korrelationen höherer Ordnung anhand der Abweichungen zwischen Original und Surrogaten finden.
"Wir konnten nicht-Gauss'sche Anteile und Asymmetrien mit hoher Signifikanz auf den größten Skalen nachweisen - es ist das erste Mal, dass nicht-Gaussianitäten mit einer derart hohen Signifikanz nachgewiesen wurden", sagt Räth. "Unsere Überprüfung systematischer Effekte hat bisher keine Erklärung dafür geliefert, so dass wir hier von einem kosmologischen Ursprung des Signals ausgehen müssen."
Für ihre Analyse nutzten die Wissenschaftler verschiedene Kombinationen der WMAP-Daten, die über 5 oder 7 Jahre hinweg gesammelt wurden, ohne oder mit Berücksichtigung bestimmter Korrekturen für Vordergrundstrahlung, um so auf systematische Fehler zu testen. Einige Signaturen auf kleinen Skalen könnten durch den Prozess der Kartenerstellung hervorgerufen sein, die Signifikanz der Ergebnisse auf großen Skalen erhöht sich allerdings, wenn die Karten ‚sauberer' werden. Noch führen die Wissenschaftler ihre Tests mit den WMAP fort. Sie werden diese Analyse aber auch auf neue Beobachtungen des CMB mit dem Planck-Satelliten anwenden, sobald diese Daten zur Verfügung stehen. Da dies ein vollständig anderes Instrument mit unabhängigen systematischen Fehlern ist, werden diese Resultate der endgültige Test für die Gültigkeit der bisher erzielten Ergebnisse sein.
letzte Änderung 2017-10-16 durch A. Agudo
